5.Ekuazio -sistemak

1 Ekuazio linealen sistemak

Ekuazio liealen sistemak deitzen diogu linea bat formatzen dutelako,eta berretzaile guztiak 1 direlako.

Bi ezezaguneko ekuazio lineala: ax + by =c   a,b eta c zenbaki errealak dira, eta x eta y,ezezagunak.
Ekuazioa betetzen duen zenbakien pare bakoitzari ebazpena deitzen diogu.

Bi ezezaguneko ekuazioek infinitu ebazpen dituzte,baina zenbaki pare batzuk ez dira ebazpenak.

Infinitu ebazpen:

2x + 3y = 2    ----->    x=1, y =0 parea ebazpena da:
                                    2 · 1 + 3 · 0 = 2
                                                                                             Ebazpen guztiak adierazteko,ebazpenak diren
                                                                                             bi puntu hartu eta zuzen batean elkartu behar
                                                                                             dira.
                                   x= -2,y =2 parea ebazpena da:
                                           2 · (-2) + 3 · 2 =2


Bi ezezaguneko ekuazio linealen sistema bat horrelako ekuazion multzo bat da eta ekuazio jorietarako ebazpen komuna kalkulkatu nahi da.
Ekuazio -sistemaren ebazpen bat ,bi ekuazioak betetzen dituen balio pare bakoitza da.


Ekuazio sistema lineala aljebraikikoki ebazterakoan hiru desberdin ditugu:

1)Sistemak soluzioa du,"bateragarria" da:

• A / Soluzio bakarra du,"bateragarria eta mugatua " da.       A2/A1 ezberdin B2/B1
• B/Infinitu soluzio ditu,"bateragarria eta mugagabea "da.      A2/A1 = B2/B1=C2/C1

2)Sistema ez du soluziorik,"bateraezina" da:

• A2/A1=B2/B1 ezberdin C2/C1

Sistema osatzen duten ekuazioak grafikoki adieraziko bagenitu hiru grafiko diferenteak aterako dira

1.a ) Bateragarri mugatua

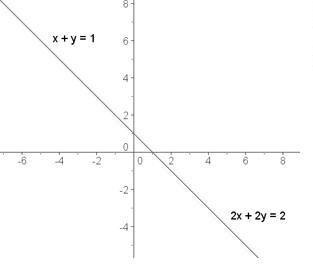
1.b)Bateragarri mugagabea 

2Bateraezina